Автор презентации
Макс Славянин
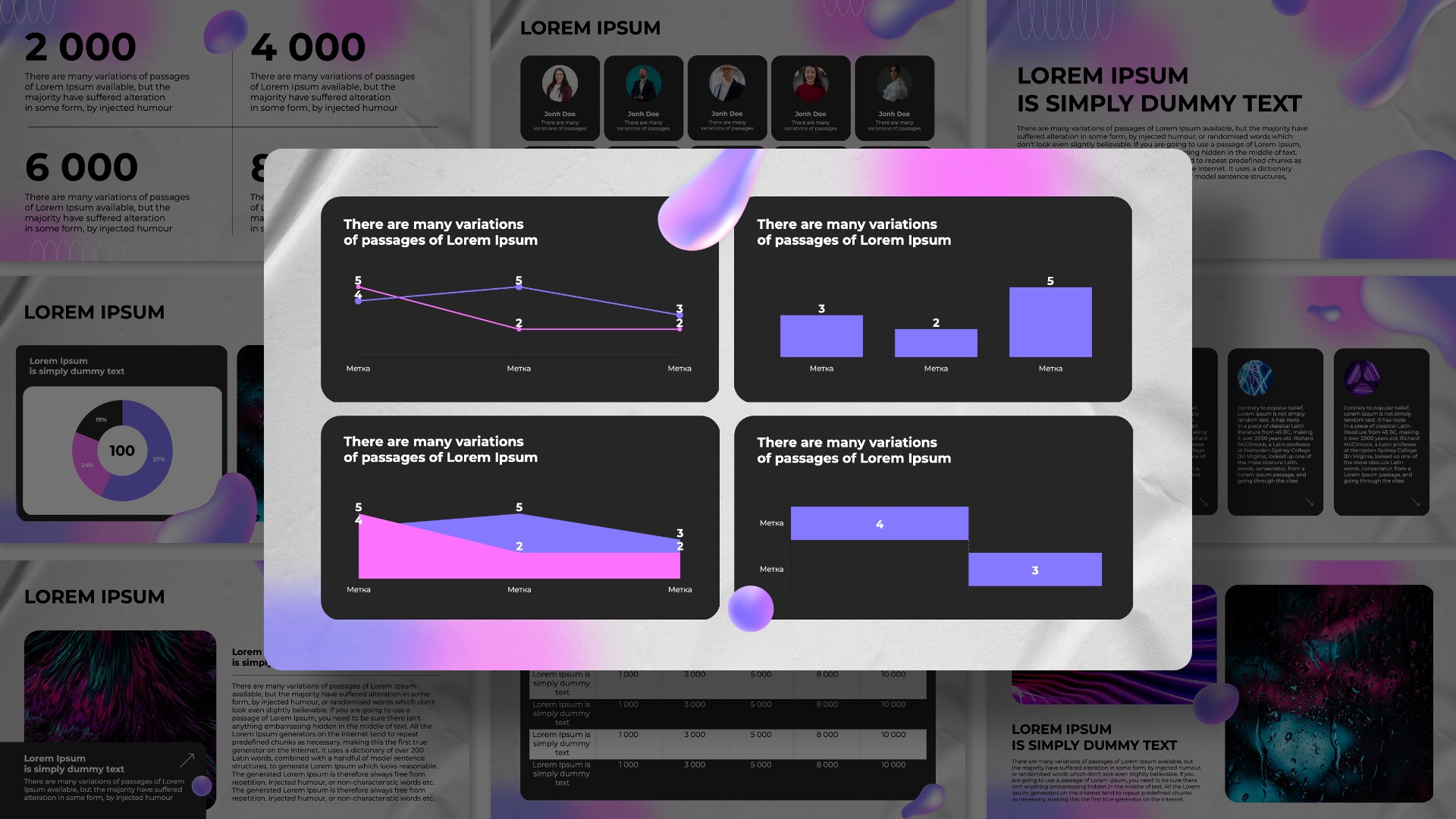
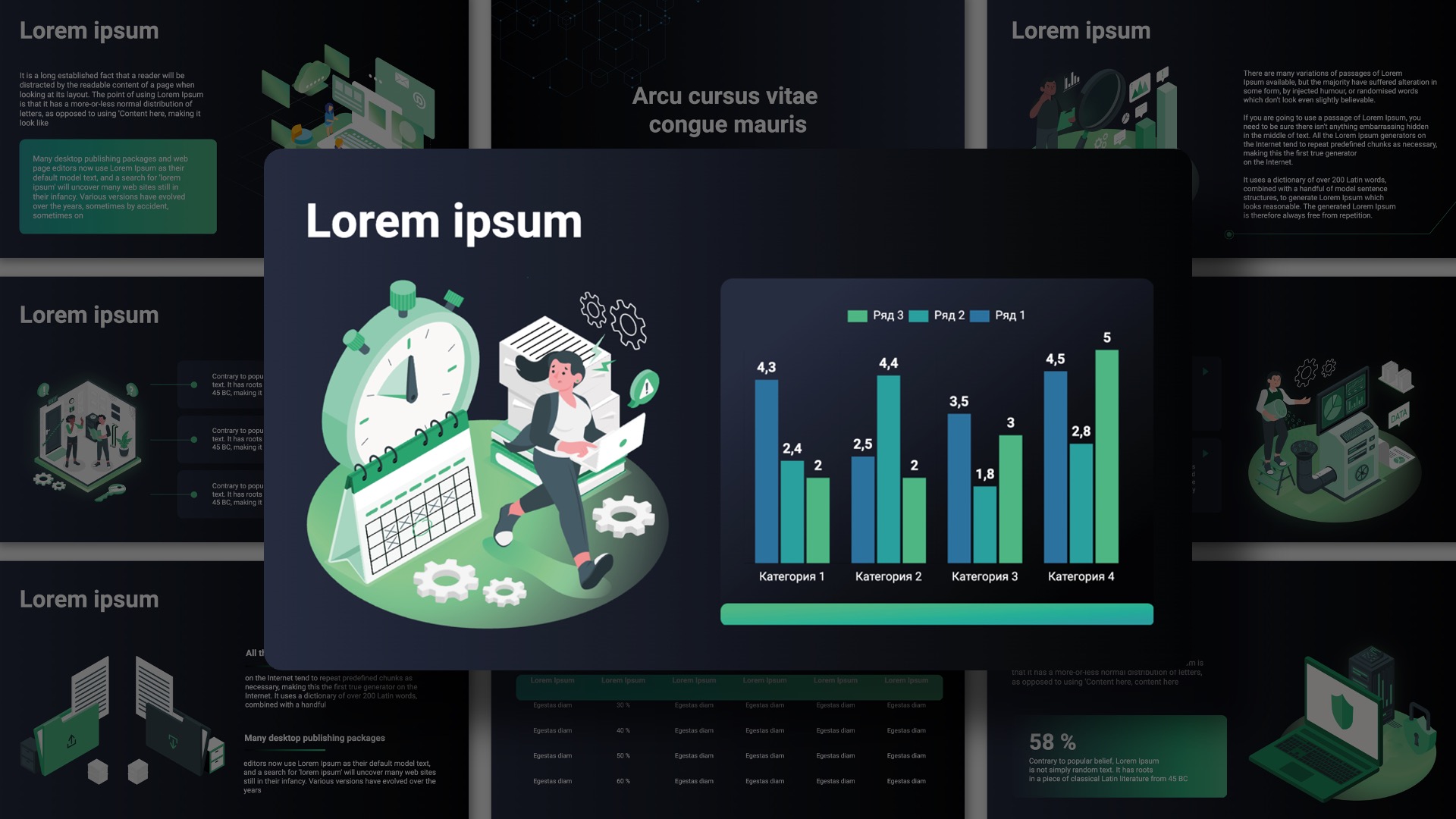
Слайд 1: Геометрические приложения кратных интегралов
Кратные интегралы позволяют вычислять объемы тел, площади поверхностей и другие геометрические параметры.
Слайд 2: Объем тела
Объем тела является одним из основных приложений кратного интеграла. Для вычисления объема V тела, ограниченного поверхностями, используется формула: V = ∫∫E ρ(x, y) dA, где E - область определения функции плотности ρ(x, y), а ρ(x, y) описывает распределение плотности внутри тела.
Слайд 3: Площадь поверхности
Определение площади поверхности. Формула для вычисления площади поверхности. Примеры применения формулы. Свойства площади поверхности. Заключение.
Слайд 4: Масса неоднородного тела
Определение массы как физической величины. Неоднородность распределения плотности вещества в теле. Использование кратных интегралов для вычисления массы. Формула для расчета массы через плотность и объем. Пример расчета массы для простого тела. Учет переменной плотности в сложных телах. Применение теоремы о среднем значении для вычислений. Понятие центра масс и его определение через кратные интегралы. Заключение: важность учета неоднородности при расчетах массы.
Слайд 5: Работа переменной силы
Работа переменной силы описывается как интеграл от функции, которая выражает силу как функцию перемещения. Этот интеграл позволяет вычислить работу, совершаемую силой вдоль некоторого пути. В случае нескольких измерений, таких как трехмерное пространство, работа переменной силы может быть выражена через тройной интеграл. Применение кратных интегралов позволяет учитывать изменение силы в пространстве и находить точное значение работы, что имеет важное значение в физике и инженерных расчетах.
Слайд 6: Центр масс
Центр масс представляет собой геометрическую точку, которая описывает движение системы многих тел под действием гравитации или других сил. Для системы n материальных точек с массами mi и координатами xi, yi, zi, центр масс определяется формулой: $$\bar{x} = \frac{\sum_{i=1}^n m_ix_i}{\sum_{i=1}^n m_i}, \quad \bar{y} = \frac{\sum_{i=1}^n m_iy_i}{\sum_{i=1}^n m_i}, \quad \bar{z} = \frac{\sum_{i=1}^n m_iz_i}{\sum_{i=1}^n m_i}$$ Эта точка является осредненной координатой всех частиц системы относительно массы и служит важным понятием в механике и астрофизике для описания движения тел.
Рекомендации для вас
Секреты классной инфографики для маркетологов
Slider — спикер на онлайн-конференции Skillbox по нейросетям!
Шаблоны презентаций
