Автор презентации
Виктория
Слайд 1: Математика и стихосложения
Математика и стихосложение тесно связаны, так как обе дисциплины требуют точности, ритма и гармонии.
Слайд 2: Введение: Математика и поэзия – необычное сочетание
Введение: Математика и поэзия - это необычное, но гармоничное сочетание логики и творчества. Поэты используют математические структуры и закономерности для создания ритма и рифмы, а математики находят вдохновение в поэзии.
Слайд 3: Математические концепции в стихосложении
Введение в математические концепции стихосложения. Определение ритма и метра в поэзии. Роль рифмы в стихотворении. Симметрия и асимметрия в структуре стиха. Использование чисел и математических формул в поэзии. Алгоритмы и шаблоны в создании стихотворений. Анализ классических примеров математических концепций в стихах. Заключение: значение математики в искусстве стихосложения.
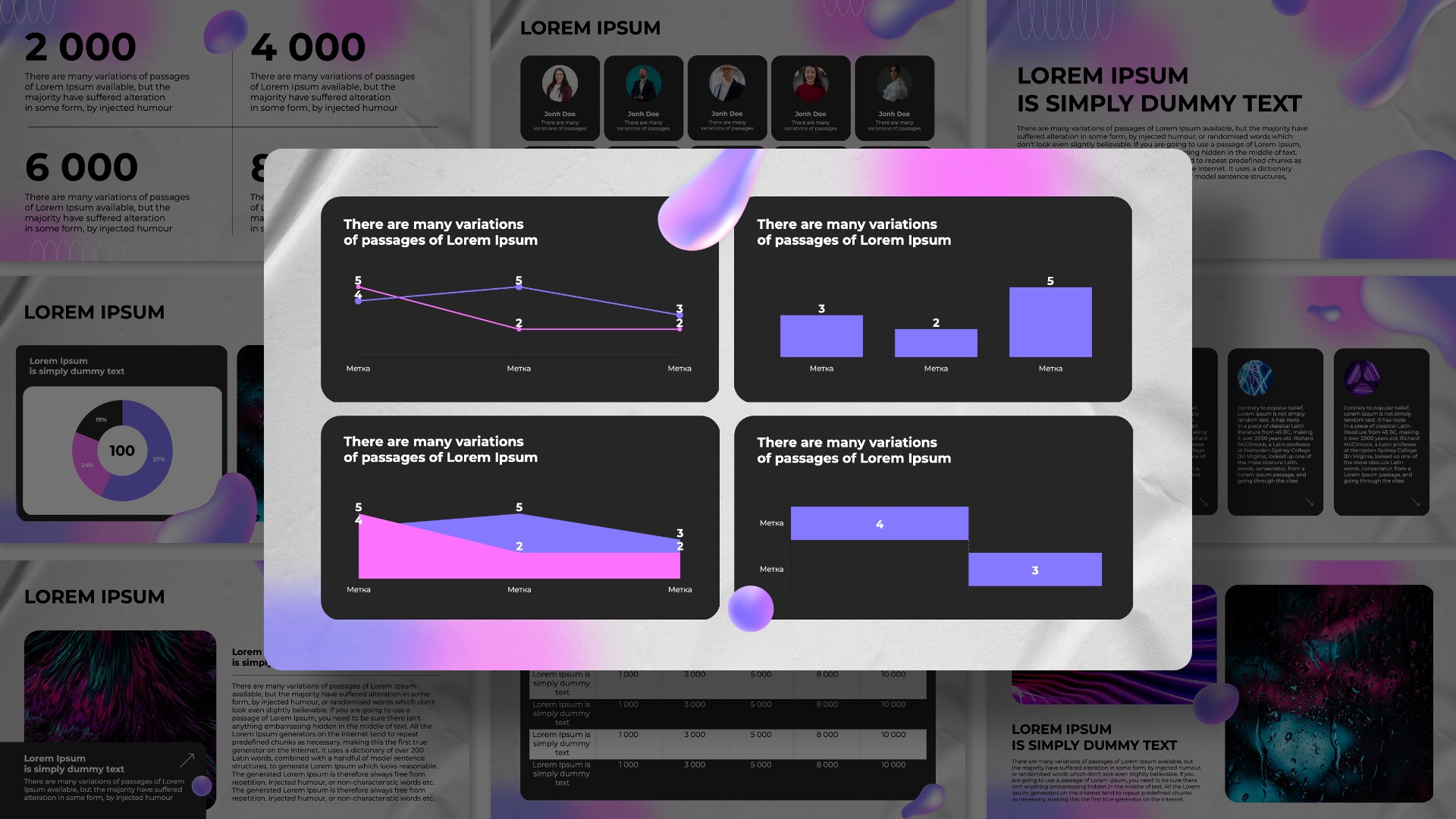
Слайд 4: Принцип золотого сечения в поэзии
Принцип золотого сечения в поэзии заключается в том, что стихотворение строится таким образом, чтобы наиболее важные элементы находились в определенных пропорциях относительно друг друга. Это создает гармоничное соотношение между формой и содержанием произведения. Например, в классическом сонете строфа из восьми строк должна быть построена так, чтобы первая половина (первые четыре строки) содержала основную мысль, а вторая половина (следующие четыре строки) развивала эту мысль. Это соответствует принципу золотого сечения, где важная информация распределяется неравномерно, создавая тем самым баланс и гармонию. Таким образом, применение принципа золотого сечения в поэзии позволяет создавать произведения, которые не только красиво звучат, но и имеют глубокий смысл и структуру.
Слайд 5: Ряды Фибоначчи, гармония и симметрия
Введение в ряды Фибоначчи и их связь с гармонией и симметрией. Определение ряда Фибоначчи и его свойства. Гармония в музыке и архитектуре, основанная на числах Фибоначчи. Симметрия в природе и искусстве, связанная с числами Фибоначчи. Примеры использования чисел Фибоначчи в дизайне и искусстве. Математические доказательства связи между числами Фибоначчи и золотым сечением. Заключение: значение рядов Фибоначчи для современной науки и искусства. Вопросы для обсуждения: применение рядов Фибоначчи в повседневной жизни.
Слайд 6: Фракталы
Фрактал Самоподобие Итерация Рекурсия Хаусдорфова размерность Примеры в природе Примеры в искусстве Математические фракталы Компьютерное моделирование Применение в науке Применение в технике Применение в финансах Применение в медицине Применение в музыке Применение в архитектуре Применение в биологии Применение в лингвистике Применение в социологии Применение в психологии Применение в философии
Слайд 7: Спасибо за внимание
Спасибо за внимание! Этот слайд завершает нашу презентацию на тему "Математика и стихосложение". Мы надеемся, что вы нашли наши идеи интересными и вдохновляющими. Если у вас есть вопросы или комментарии, мы будем рады ответить на них позже.
Рекомендации для вас
8 сервисов и приложений для эффективных уроков + нейросети
Нейросеть против человека: кто сделает презентацию лучше?
Шаблоны презентаций
